The distribution of acoustic energy within an enclosure is directly influenced by structural design. From the ornate ceiling of a cathedral to the strategically placed panels inside a concert hall, there are a variety of different practical techniques used to guide and optimize the acoustic performance. If not properly addressed however, mistreated interiors can vary the sound field resulting in not only undesirable but also harmful conditions. The mathematical modeling of such a highly reverberant field is of great interest to engineers and has led to several new modeling techniques over the past century. Conclusions drawn from these models have been used to predict sound fields and avoid dangerous situations, such as identifying potential `hot spots' that pose risks to habitability, as well as to enhance our understanding of the physical phenomena that govern the acoustic interactions between a field and its surroundings.
Our research is focused on the modeling of sound fields in the high frequency region (small wavelength in relation to characteristic enclosure length), a notoriously difficult limit when dealing with highly reverberant fields. The combination of irregular wall geometries, non-uniform boundary conditions and highly directional interior sources form challenges that are usually confronted with frequency dependent numerical methods such as finite element packages. These more traditional approaches quickly become computationally expensive when handling the dense resonant frequency bands in the high frequency limit.
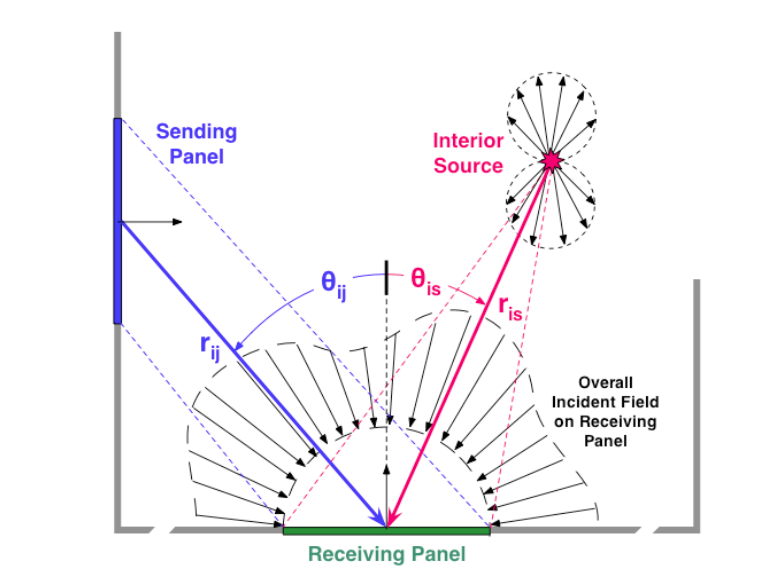
The modeling technique developed by our group is called the Energy Intensity Boundary Element Method (EIBEM). Derived from first principles, this technique formulates an integral equation that governs the spatial distribution of broadband acoustic energy inside an enclosure. The resulting energy equation is solved using a boundary element algorithm which discretizes the enclosure boundary into energy intensity source panels allowing for both diffuse and specular reflection boundary conditions. Energy distributions are both studied and verified for rectangular, cylindrical and spherical enclosures. Insight gained from these studies has led to the development of absorption scaling theory, an asymptotic analysis of absorption distribution along reflective boundaries, and has applications in room design, inverse problem research and underwater scattering.
Selected References
Michalis, K. "Modeling Specular and Diffuse Reflection Sound Fields in Enclosures with an Energy-Intensity Boundary Element Method" (PhD Thesis, Duke University, 2011).